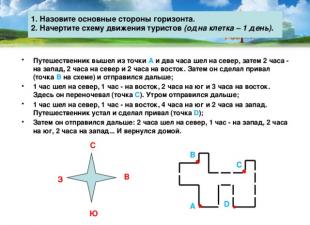
Материал из Википедии - свободной энциклопедии

Ве́кторное (или лине́йное ) простра́нство - математическая структура , которая представляет собой набор элементов, называемых векторами , для которых определены операции сложения друг с другом и умножения на число - скаляр . Эти операции подчинены восьми аксиомам. Скаляры могут быть элементами вещественного , комплексного или любого другого поля чисел . Частным случаем подобного пространства является обычное трехмерное евклидово пространство, векторы которого используются, к примеру, для представления физических сил . При этом следует отметить, что вектор как элемент векторного пространства не обязательно должен быть задан в виде направленного отрезка . Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы .

Векторные пространства являются предметом изучения линейной алгебры . Одна из главных характеристик векторного пространства - его размерность. Размерность представляет собой максимальное число линейно независимых элементов пространства, то есть, прибегая к грубому геометрическому описанию, число направлений, невыразимых друг через друга посредством только операций сложения и умножения на скаляр. Векторное пространство можно наделить дополнительными структурами, например, нормой или скалярным произведением . Подобные пространства естественным образом появляются в математическом анализе , преимущественно в виде бесконечномерных функциональных пространств (англ. ), где в качестве векторов выступают функции . Многие проблемы анализа требуют выяснить, сходится ли последовательность векторов к данному вектору. Рассмотрение таких вопросов возможно в векторных пространствах с дополнительной структурой, в большинстве случаев - подходящей топологией , что позволяет определить понятия близости и непрерывности . Такие топологические векторные пространства , в частности, банаховы и гильбертовы , допускают более глубокое изучение.

Кроме векторов, линейная алгебра изучает также тензоры более высокого ранга (скаляр считается тензором ранга 0, вектор - тензором ранга 1).

Первые труды, предвосхитившие введение понятия векторного пространства, относятся к XVII веку . Именно тогда своё развитие получили аналитическая геометрия , учения о матрицах , системах линейных уравнений , евклидовых векторах .

Определение

Линейное , или векторное пространство $V\; \backslash left(F\; \backslash right)$ над полем $F$ - это упорядоченная четвёрка $(V,F,+,\backslash cdot)$, где

• $V$ - непустое множество элементов произвольной природы, которые называются векторами ;
• $F$ - (алгебраическое) поле, элементы которого называются скалярами ;
• Определена операция сложения векторов $V\backslash times\; V\backslash to\; V$, сопоставляющая каждой паре элементов $\backslash mathbf\{x\},\; \backslash mathbf\{y\}$ множества $V$ $V$, называемый их суммой и обозначаемый $\backslash mathbf\{x\}\; +\; \backslash mathbf\{y\}$;
• Определена операция умножения векторов на скаляры $F\backslash times\; V\backslash to\; V$, сопоставляющая каждому элементу $\backslash lambda$ поля $F$ и каждому элементу $\backslash mathbf\{x\}$ множества $V$ единственный элемент множества $V$, обозначаемый $\backslash lambda\backslash cdot\; \backslash mathbf\{x\}$ или $\backslash lambda\backslash mathbf\{x\}$;

Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами (например, множество пар действительных чисел $\backslash mathbb\{R\}^2$ может быть двумерным векторным пространством над полем действительных чисел либо одномерным - над полем комплексных чисел).

Простейшие свойства

1. Векторное пространство является абелевой группой по сложению.
2. Нейтральный элемент $\backslash mathbf\{0\}\; \backslash in\; V$
3. $0\backslash cdot\backslash mathbf\{x\}\; =\; \backslash mathbf\{0\}$ для любого $\backslash mathbf\{x\}\; \backslash in\; V$.
4. Для любого $\backslash mathbf\{x\}\; \backslash in\; V$ противоположный элемент $-\backslash mathbf\{x\}\; \backslash in\; V$ является единственным, что вытекает из групповых свойств.
5. $1\backslash cdot\backslash mathbf\{x\}\; =\; \backslash mathbf\{x\}$ для любого $\backslash mathbf\{x\}\; \backslash in\; V$.
6. $(-\backslash alpha)\backslash cdot\backslash mathbf\{x\}\; =\; \backslash alpha\backslash cdot(-\backslash mathbf\{x\})\; =\; -(\backslash alpha\backslash mathbf\{x\})$ для любых $\backslash alpha\; \backslash in\; F$ и $\backslash mathbf\{x\}\; \backslash in\; V$.
7. $\backslash alpha\backslash cdot\; \backslash mathbf\{0\}\; =\; \backslash mathbf\{0\}$ для любого $\backslash alpha\; \backslash in\; F$.

Связанные определения и свойства

Подпространство

Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество $K$ линейного пространства $V$ такое, что $K$ само является линейным пространством по отношению к определенным в $V$ действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как $\backslash mathrm\{Lat\}(V)$. Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

1. для всякого вектора $\backslash mathbf\{x\}\backslash in\; K$, вектор $\backslash alpha\backslash mathbf\{x\}$ также принадлежал $K$, при любом $\backslash alpha\backslash in\; F$;
2. для всяких векторов $\backslash mathbf\{x\},\; \backslash mathbf\{y\}\; \backslash in\; K$, вектор $\backslash mathbf\{x\}+\backslash mathbf\{y\}$ также принадлежал $K$.

Последние два утверждения эквивалентны следующему:

Для всяких векторов $\backslash mathbf\{x\},\; \backslash mathbf\{y\}\; \backslash in\; K$, вектор $\backslash alpha\backslash mathbf\{x\}+\backslash beta\backslash mathbf\{y\}$ также принадлежал $K$ для любых $\backslash alpha,\; \backslash beta\; \backslash in\; F$.

В частности, векторное пространство, состоящее из одного лишь нулевого вектора, является подпространством любого пространства; любое пространство является подпространством самого себя. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными .

Свойства подпространств

• Пересечение любого семейства подпространств - снова подпространство;
• Сумма подпространств $\backslash \{K\_i\backslash quad|\backslash quad\; i\; \backslash in\; 1\backslash ldots\; N\backslash \}$ определяется как множество, содержащее всевозможные суммы элементов $K\_i$: $\backslash sum\_\{i=1\}^N\; \{K\_i\}:=\; \backslash \{\backslash mathbf\{x\}\_1\; +\; \backslash mathbf\{x\}\_2\; +\; \backslash ldots\; +\; \backslash mathbf\{x\}\_N\backslash quad|\backslash quad\; \backslash mathbf\{x\}\_i\; \backslash in\; K\_i\backslash quad\; (i\backslash in\; 1\backslash ldots\; N)\backslash \}$.
  • Сумма конечного семейства подпространств - снова подпространство.

Линейные комбинации

Конечная сумма вида

$\backslash alpha\_1\backslash mathbf\{x\}\_1\; +\; \backslash alpha\_2\backslash mathbf\{x\}\_2\; +\; \backslash ldots\; +\; \backslash alpha\_n\backslash mathbf\{x\}\_n$

Линейная комбинация называется:

Базис. Размерность

Векторы $\backslash mathbf\{x\}\_1,\; \backslash mathbf\{x\}\_2,\; \backslash ldots,\; \backslash mathbf\{x\}\_n$ называются линейно зависимыми , если существует их нетривиальная линейная комбинация, равная нулю:

$\backslash alpha\_1\backslash mathbf\{x\}\_1\; +\; \backslash alpha\_2\backslash mathbf\{x\}\_2\; +\; \backslash ldots\; +\; \backslash alpha\_n\backslash mathbf\{x\}\_n\; =\; \backslash mathbf\{0\},\; \backslash quad\; \backslash \; |\backslash alpha\_1|\; +\; |\backslash alpha\_2|\; +\; \backslash ldots\; +\; |\backslash alpha\_n|\; \backslash neq\; 0.$

В противном случае эти векторы называются линейно независимыми .

Данное определение допускает следующее обобщение: бесконечное множество векторов из $V$ называется линейно зависимым , если линейно зависимо некоторое конечное его подмножество, и линейно независимым , если любое его конечное подмножество линейно независимо.

Свойства базиса:

• Любые $n$ линейно независимых элементов $n$-мерного пространства образуют базис этого пространства.
• Любой вектор $\backslash mathbf\{x\}\; \backslash in\; V$ можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:

$\backslash mathbf\{x\}\; =\; \backslash alpha\_1\backslash mathbf\{x\}\_1\; +\; \backslash alpha\_2\backslash mathbf\{x\}\_2\; +\; \backslash ldots\; +\; \backslash alpha\_n\backslash mathbf\{x\}\_n$.

Линейная оболочка

Линейная оболочка $\backslash mathcal\; V(X)$ подмножества $X$ линейного пространства $V$ - пересечение всех подпространств $V$, содержащих $X$.

Линейная оболочка является подпространством $V$.

Линейная оболочка также называется подпространством, порожденным $X$. Говорят также, что линейная оболочка $\backslash mathcal\; V(X)$ - пространство, натянутое на множество $X$.

Линейная оболочка $\backslash mathcal\; V(X)$ состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из $X$. В частности, если $X$ - конечное множество, то $\backslash mathcal\; V(X)$ состоит из всех линейных комбинаций элементов $X$. Таким образом, нулевой вектор всегда принадлежит линейной оболочке.

Если $X$ - линейно независимое множество, то оно является базисом $\backslash mathcal\; V(X)$ и тем самым определяет его размерность.

Примеры

• Нулевое пространство, единственным элементом которого является ноль.
• Пространство всех функций $X\backslash to\; F$ с конечным носителем образует векторное пространство размерности равной мощности $X$.
• Поле действительных чисел может быть рассмотрено как континуально -мерное векторное пространство над полем рациональных чисел .
• Любое поле является одномерным пространством над собой.

Дополнительные структуры

См. также

Напишите отзыв о статье "Векторное пространство"

Примечания

Литература

• Гельфанд И. М. Лекции по линейной алгебре. - 5-е. - М .: Добросвет, МЦНМО , 1998. - 319 с. - ISBN 5-7913-0015-8 .
• Гельфанд И. М. Лекции по линейной алгебре. 5-е изд. - М .: Добросвет, МЦНМО, 1998. - 320 с. - ISBN 5-7913-0016-6 .
• Кострикин А. И. , Манин Ю. И. Линейная алгебра и геометрия. 2-е изд. - М .: Наука , 1986. - 304 с.
• Кострикин А. И. Введение в алгебру. Ч. 2: Линейная алгебра. - 3-е. - М .: Наука ., 2004. - 368 с. - (Университетский учебник).
• Мальцев А. И. Основы линейной алгебры. - 3-е. - М .: Наука , 1970. - 400 с.

• Постников М. М. Линейная алгебра (Лекции по геометрии. Семестр II). - 2-е. - М .: Наука , 1986. - 400 с.
• Стренг Г. Линейная алгебра и её применения = Linear Algebra and Its Applications. - М .: Мир , 1980. - 454 с.
• Ильин В. А., Позняк Э. Г. Линейная алгебра. 6-е изд. - М .: Физматлит, 2010. - 280 с. - ISBN 978-5-9221-0481-4 .
• Халмош П. Конечномерные векторные пространства = Finite-Dimensional Vector Spaces. - М .: Физматгиз , 1963. - 263 с.
• Фаддеев Д. К. Лекции по алгебре. - 5-е. - СПб. : Лань , 2007. - 416 с.
• Шафаревич И. Р. , Ремизов А. О. Линейная алгебра и геометрия. - 1-е. - М .: Физматлит , 2009. - 511 с.
• Шрейер О., Шпернер Г. Введение в линейную алгебру в геометрическом изложении = Einfuhrung in die analytische Geometrie und Algebra / Ольшанский Г. (перевод с немецкого). - М.–Л.: ОНТИ , 1934. - 210 с.

Векторы и матрицы Векторы Основные понятия Виды векторов Операции над векторами Типы пространств Матрицы Основные понятия Другое

Отрывок, характеризующий Векторное пространство

Кутузов прошел по рядам, изредка останавливаясь и говоря по нескольку ласковых слов офицерам, которых он знал по турецкой войне, а иногда и солдатам. Поглядывая на обувь, он несколько раз грустно покачивал головой и указывал на нее австрийскому генералу с таким выражением, что как бы не упрекал в этом никого, но не мог не видеть, как это плохо. Полковой командир каждый раз при этом забегал вперед, боясь упустить слово главнокомандующего касательно полка. Сзади Кутузова, в таком расстоянии, что всякое слабо произнесенное слово могло быть услышано, шло человек 20 свиты. Господа свиты разговаривали между собой и иногда смеялись. Ближе всех за главнокомандующим шел красивый адъютант. Это был князь Болконский. Рядом с ним шел его товарищ Несвицкий, высокий штаб офицер, чрезвычайно толстый, с добрым, и улыбающимся красивым лицом и влажными глазами; Несвицкий едва удерживался от смеха, возбуждаемого черноватым гусарским офицером, шедшим подле него. Гусарский офицер, не улыбаясь, не изменяя выражения остановившихся глаз, с серьезным лицом смотрел на спину полкового командира и передразнивал каждое его движение. Каждый раз, как полковой командир вздрагивал и нагибался вперед, точно так же, точь в точь так же, вздрагивал и нагибался вперед гусарский офицер. Несвицкий смеялся и толкал других, чтобы они смотрели на забавника.
Кутузов шел медленно и вяло мимо тысячей глаз, которые выкатывались из своих орбит, следя за начальником. Поровнявшись с 3 й ротой, он вдруг остановился. Свита, не предвидя этой остановки, невольно надвинулась на него.
– А, Тимохин! – сказал главнокомандующий, узнавая капитана с красным носом, пострадавшего за синюю шинель.
Казалось, нельзя было вытягиваться больше того, как вытягивался Тимохин, в то время как полковой командир делал ему замечание. Но в эту минуту обращения к нему главнокомандующего капитан вытянулся так, что, казалось, посмотри на него главнокомандующий еще несколько времени, капитан не выдержал бы; и потому Кутузов, видимо поняв его положение и желая, напротив, всякого добра капитану, поспешно отвернулся. По пухлому, изуродованному раной лицу Кутузова пробежала чуть заметная улыбка.
– Еще измайловский товарищ, – сказал он. – Храбрый офицер! Ты доволен им? – спросил Кутузов у полкового командира.
И полковой командир, отражаясь, как в зеркале, невидимо для себя, в гусарском офицере, вздрогнул, подошел вперед и отвечал:
– Очень доволен, ваше высокопревосходительство.
– Мы все не без слабостей, – сказал Кутузов, улыбаясь и отходя от него. – У него была приверженность к Бахусу.
Полковой командир испугался, не виноват ли он в этом, и ничего не ответил. Офицер в эту минуту заметил лицо капитана с красным носом и подтянутым животом и так похоже передразнил его лицо и позу, что Несвицкий не мог удержать смеха.
Кутузов обернулся. Видно было, что офицер мог управлять своим лицом, как хотел: в ту минуту, как Кутузов обернулся, офицер успел сделать гримасу, а вслед за тем принять самое серьезное, почтительное и невинное выражение.
Третья рота была последняя, и Кутузов задумался, видимо припоминая что то. Князь Андрей выступил из свиты и по французски тихо сказал:
– Вы приказали напомнить о разжалованном Долохове в этом полку.
– Где тут Долохов? – спросил Кутузов.
Долохов, уже переодетый в солдатскую серую шинель, не дожидался, чтоб его вызвали. Стройная фигура белокурого с ясными голубыми глазами солдата выступила из фронта. Он подошел к главнокомандующему и сделал на караул.
– Претензия? – нахмурившись слегка, спросил Кутузов.
– Это Долохов, – сказал князь Андрей.
– A! – сказал Кутузов. – Надеюсь, что этот урок тебя исправит, служи хорошенько. Государь милостив. И я не забуду тебя, ежели ты заслужишь.
Голубые ясные глаза смотрели на главнокомандующего так же дерзко, как и на полкового командира, как будто своим выражением разрывая завесу условности, отделявшую так далеко главнокомандующего от солдата.
– Об одном прошу, ваше высокопревосходительство, – сказал он своим звучным, твердым, неспешащим голосом. – Прошу дать мне случай загладить мою вину и доказать мою преданность государю императору и России.
Кутузов отвернулся. На лице его промелькнула та же улыбка глаз, как и в то время, когда он отвернулся от капитана Тимохина. Он отвернулся и поморщился, как будто хотел выразить этим, что всё, что ему сказал Долохов, и всё, что он мог сказать ему, он давно, давно знает, что всё это уже прискучило ему и что всё это совсем не то, что нужно. Он отвернулся и направился к коляске.
Полк разобрался ротами и направился к назначенным квартирам невдалеке от Браунау, где надеялся обуться, одеться и отдохнуть после трудных переходов.
– Вы на меня не претендуете, Прохор Игнатьич? – сказал полковой командир, объезжая двигавшуюся к месту 3 ю роту и подъезжая к шедшему впереди ее капитану Тимохину. Лицо полкового командира выражало после счастливо отбытого смотра неудержимую радость. – Служба царская… нельзя… другой раз во фронте оборвешь… Сам извинюсь первый, вы меня знаете… Очень благодарил! – И он протянул руку ротному.
– Помилуйте, генерал, да смею ли я! – отвечал капитан, краснея носом, улыбаясь и раскрывая улыбкой недостаток двух передних зубов, выбитых прикладом под Измаилом.
– Да господину Долохову передайте, что я его не забуду, чтоб он был спокоен. Да скажите, пожалуйста, я всё хотел спросить, что он, как себя ведет? И всё…
– По службе очень исправен, ваше превосходительство… но карахтер… – сказал Тимохин.
– А что, что характер? – спросил полковой командир.
– Находит, ваше превосходительство, днями, – говорил капитан, – то и умен, и учен, и добр. А то зверь. В Польше убил было жида, изволите знать…
– Ну да, ну да, – сказал полковой командир, – всё надо пожалеть молодого человека в несчастии. Ведь большие связи… Так вы того…
– Слушаю, ваше превосходительство, – сказал Тимохин, улыбкой давая чувствовать, что он понимает желания начальника.
– Ну да, ну да.
Полковой командир отыскал в рядах Долохова и придержал лошадь.
– До первого дела – эполеты, – сказал он ему.
Долохов оглянулся, ничего не сказал и не изменил выражения своего насмешливо улыбающегося рта.
– Ну, вот и хорошо, – продолжал полковой командир. – Людям по чарке водки от меня, – прибавил он, чтобы солдаты слышали. – Благодарю всех! Слава Богу! – И он, обогнав роту, подъехал к другой.
– Что ж, он, право, хороший человек; с ним служить можно, – сказал Тимохин субалтерн офицеру, шедшему подле него.
– Одно слово, червонный!… (полкового командира прозвали червонным королем) – смеясь, сказал субалтерн офицер.
Счастливое расположение духа начальства после смотра перешло и к солдатам. Рота шла весело. Со всех сторон переговаривались солдатские голоса.
– Как же сказывали, Кутузов кривой, об одном глазу?
– А то нет! Вовсе кривой.
– Не… брат, глазастее тебя. Сапоги и подвертки – всё оглядел…
– Как он, братец ты мой, глянет на ноги мне… ну! думаю…
– А другой то австрияк, с ним был, словно мелом вымазан. Как мука, белый. Я чай, как амуницию чистят!
– Что, Федешоу!… сказывал он, что ли, когда стражения начнутся, ты ближе стоял? Говорили всё, в Брунове сам Бунапарте стоит.
– Бунапарте стоит! ишь врет, дура! Чего не знает! Теперь пруссак бунтует. Австрияк его, значит, усмиряет. Как он замирится, тогда и с Бунапартом война откроется. А то, говорит, в Брунове Бунапарте стоит! То то и видно, что дурак. Ты слушай больше.
– Вишь черти квартирьеры! Пятая рота, гляди, уже в деревню заворачивает, они кашу сварят, а мы еще до места не дойдем.
– Дай сухарика то, чорт.
– А табаку то вчера дал? То то, брат. Ну, на, Бог с тобой.
– Хоть бы привал сделали, а то еще верст пять пропрем не емши.
– То то любо было, как немцы нам коляски подавали. Едешь, знай: важно!
– А здесь, братец, народ вовсе оголтелый пошел. Там всё как будто поляк был, всё русской короны; а нынче, брат, сплошной немец пошел.
– Песенники вперед! – послышался крик капитана.
И перед роту с разных рядов выбежало человек двадцать. Барабанщик запевало обернулся лицом к песенникам, и, махнув рукой, затянул протяжную солдатскую песню, начинавшуюся: «Не заря ли, солнышко занималося…» и кончавшуюся словами: «То то, братцы, будет слава нам с Каменскиим отцом…» Песня эта была сложена в Турции и пелась теперь в Австрии, только с тем изменением, что на место «Каменскиим отцом» вставляли слова: «Кутузовым отцом».
Оторвав по солдатски эти последние слова и махнув руками, как будто он бросал что то на землю, барабанщик, сухой и красивый солдат лет сорока, строго оглянул солдат песенников и зажмурился. Потом, убедившись, что все глаза устремлены на него, он как будто осторожно приподнял обеими руками какую то невидимую, драгоценную вещь над головой, подержал ее так несколько секунд и вдруг отчаянно бросил ее:
Ах, вы, сени мои, сени!
«Сени новые мои…», подхватили двадцать голосов, и ложечник, несмотря на тяжесть амуниции, резво выскочил вперед и пошел задом перед ротой, пошевеливая плечами и угрожая кому то ложками. Солдаты, в такт песни размахивая руками, шли просторным шагом, невольно попадая в ногу. Сзади роты послышались звуки колес, похрускиванье рессор и топот лошадей.
Кутузов со свитой возвращался в город. Главнокомандующий дал знак, чтобы люди продолжали итти вольно, и на его лице и на всех лицах его свиты выразилось удовольствие при звуках песни, при виде пляшущего солдата и весело и бойко идущих солдат роты. Во втором ряду, с правого фланга, с которого коляска обгоняла роты, невольно бросался в глаза голубоглазый солдат, Долохов, который особенно бойко и грациозно шел в такт песни и глядел на лица проезжающих с таким выражением, как будто он жалел всех, кто не шел в это время с ротой. Гусарский корнет из свиты Кутузова, передразнивавший полкового командира, отстал от коляски и подъехал к Долохову.
Гусарский корнет Жерков одно время в Петербурге принадлежал к тому буйному обществу, которым руководил Долохов. За границей Жерков встретил Долохова солдатом, но не счел нужным узнать его. Теперь, после разговора Кутузова с разжалованным, он с радостью старого друга обратился к нему:
– Друг сердечный, ты как? – сказал он при звуках песни, ровняя шаг своей лошади с шагом роты.
– Я как? – отвечал холодно Долохов, – как видишь.
Бойкая песня придавала особенное значение тону развязной веселости, с которой говорил Жерков, и умышленной холодности ответов Долохова.
– Ну, как ладишь с начальством? – спросил Жерков.
– Ничего, хорошие люди. Ты как в штаб затесался?
– Прикомандирован, дежурю.
Они помолчали.
«Выпускала сокола да из правого рукава», говорила песня, невольно возбуждая бодрое, веселое чувство. Разговор их, вероятно, был бы другой, ежели бы они говорили не при звуках песни.
– Что правда, австрийцев побили? – спросил Долохов.
– А чорт их знает, говорят.
– Я рад, – отвечал Долохов коротко и ясно, как того требовала песня.
– Что ж, приходи к нам когда вечерком, фараон заложишь, – сказал Жерков.
– Или у вас денег много завелось?
– Приходи.
– Нельзя. Зарок дал. Не пью и не играю, пока не произведут.
– Да что ж, до первого дела…
– Там видно будет.
Опять они помолчали.
– Ты заходи, коли что нужно, все в штабе помогут… – сказал Жерков.
Долохов усмехнулся.
– Ты лучше не беспокойся. Мне что нужно, я просить не стану, сам возьму.
– Да что ж, я так…
– Ну, и я так.
– Прощай.
– Будь здоров…
… и высоко, и далеко,
На родиму сторону…
Жерков тронул шпорами лошадь, которая раза три, горячась, перебила ногами, не зная, с какой начать, справилась и поскакала, обгоняя роту и догоняя коляску, тоже в такт песни.

Возвратившись со смотра, Кутузов, сопутствуемый австрийским генералом, прошел в свой кабинет и, кликнув адъютанта, приказал подать себе некоторые бумаги, относившиеся до состояния приходивших войск, и письма, полученные от эрцгерцога Фердинанда, начальствовавшего передовою армией. Князь Андрей Болконский с требуемыми бумагами вошел в кабинет главнокомандующего. Перед разложенным на столе планом сидели Кутузов и австрийский член гофкригсрата.
– А… – сказал Кутузов, оглядываясь на Болконского, как будто этим словом приглашая адъютанта подождать, и продолжал по французски начатый разговор.
– Я только говорю одно, генерал, – говорил Кутузов с приятным изяществом выражений и интонации, заставлявшим вслушиваться в каждое неторопливо сказанное слово. Видно было, что Кутузов и сам с удовольствием слушал себя. – Я только одно говорю, генерал, что ежели бы дело зависело от моего личного желания, то воля его величества императора Франца давно была бы исполнена. Я давно уже присоединился бы к эрцгерцогу. И верьте моей чести, что для меня лично передать высшее начальство армией более меня сведущему и искусному генералу, какими так обильна Австрия, и сложить с себя всю эту тяжкую ответственность для меня лично было бы отрадой. Но обстоятельства бывают сильнее нас, генерал.
И Кутузов улыбнулся с таким выражением, как будто он говорил: «Вы имеете полное право не верить мне, и даже мне совершенно всё равно, верите ли вы мне или нет, но вы не имеете повода сказать мне это. И в этом то всё дело».
Австрийский генерал имел недовольный вид, но не мог не в том же тоне отвечать Кутузову.
– Напротив, – сказал он ворчливым и сердитым тоном, так противоречившим лестному значению произносимых слов, – напротив, участие вашего превосходительства в общем деле высоко ценится его величеством; но мы полагаем, что настоящее замедление лишает славные русские войска и их главнокомандующих тех лавров, которые они привыкли пожинать в битвах, – закончил он видимо приготовленную фразу.
Кутузов поклонился, не изменяя улыбки.
– А я так убежден и, основываясь на последнем письме, которым почтил меня его высочество эрцгерцог Фердинанд, предполагаю, что австрийские войска, под начальством столь искусного помощника, каков генерал Мак, теперь уже одержали решительную победу и не нуждаются более в нашей помощи, – сказал Кутузов.
Генерал нахмурился. Хотя и не было положительных известий о поражении австрийцев, но было слишком много обстоятельств, подтверждавших общие невыгодные слухи; и потому предположение Кутузова о победе австрийцев было весьма похоже на насмешку. Но Кутузов кротко улыбался, всё с тем же выражением, которое говорило, что он имеет право предполагать это. Действительно, последнее письмо, полученное им из армии Мака, извещало его о победе и о самом выгодном стратегическом положении армии.
– Дай ка сюда это письмо, – сказал Кутузов, обращаясь к князю Андрею. – Вот изволите видеть. – И Кутузов, с насмешливою улыбкой на концах губ, прочел по немецки австрийскому генералу следующее место из письма эрцгерцога Фердинанда: «Wir haben vollkommen zusammengehaltene Krafte, nahe an 70 000 Mann, um den Feind, wenn er den Lech passirte, angreifen und schlagen zu konnen. Wir konnen, da wir Meister von Ulm sind, den Vortheil, auch von beiden Uferien der Donau Meister zu bleiben, nicht verlieren; mithin auch jeden Augenblick, wenn der Feind den Lech nicht passirte, die Donau ubersetzen, uns auf seine Communikations Linie werfen, die Donau unterhalb repassiren und dem Feinde, wenn er sich gegen unsere treue Allirte mit ganzer Macht wenden wollte, seine Absicht alabald vereitelien. Wir werden auf solche Weise den Zeitpunkt, wo die Kaiserlich Ruseische Armee ausgerustet sein wird, muthig entgegenharren, und sodann leicht gemeinschaftlich die Moglichkeit finden, dem Feinde das Schicksal zuzubereiten, so er verdient». [Мы имеем вполне сосредоточенные силы, около 70 000 человек, так что мы можем атаковать и разбить неприятеля в случае переправы его через Лех. Так как мы уже владеем Ульмом, то мы можем удерживать за собою выгоду командования обоими берегами Дуная, стало быть, ежеминутно, в случае если неприятель не перейдет через Лех, переправиться через Дунай, броситься на его коммуникационную линию, ниже перейти обратно Дунай и неприятелю, если он вздумает обратить всю свою силу на наших верных союзников, не дать исполнить его намерение. Таким образом мы будем бодро ожидать времени, когда императорская российская армия совсем изготовится, и затем вместе легко найдем возможность уготовить неприятелю участь, коей он заслуживает».]

Головизин В.В. Лекции по алгебре и геометрии. 4

Лекции по алгебре и геометрии. Семестр 2.

Лекция 22. Векторные пространства.

Краткое содержание: определение векторного пространства, его простейшие свойства, системы векторов, линейная комбинация системы векторов, тривиальная и нетривиальная линейная комбинация, линейно зависимые и независимые системы векторов, условия линейной зависимости или независимости системы векторов, подсистемы системы векторов, системы столбцов арифметического векторного пространства.

п.1. Определение векторного пространства и его простейшие свойства.

Здесь, для удобства читателя, мы повторяем содержание п.13 лекции 1.

Определение. Пусть - произвольное непустое множество, элементы которого мы будем называть векторами, K – поле, элементы которого мы будем называть скалярами. Пусть на множестве определена внутренняя бинарная алгебраическая операция, которую мы будем обозначать знаком + и называть сложением векторов. Пусть также на множестве определена внешняя бинарная алгебраическая операция, которую мы будем называть умножением вектора на скаляр и обозначать знаком умножения. Другими словами определены два отображения:

Множество вместе с этими двумя алгебраическими операциями называется векторным пространством над полем К, если выполняются следующие аксиомы:

1. Сложение ассоциативно, т.е.

2. Существует нулевой вектор, т.е.

3. Для любого вектора существует противоположный ему:

Вектор у, противоположный вектору х, обычно обозначается –х, так что

4. Сложение коммутативно, т.е. .

5. Умножение вектора на скаляр подчиняется закону ассоциативности, т.е.

где произведение есть произведение скаляров, определенное в поле К.

6. , где 1 - это единица поля К.

7. Умножение вектора на скаляр дистрибутивно относительно сложения векторов:

8. Умножение вектора на скаляр дистрибутивно относительно сложения скаляров: .

Определение. Векторное пространство над полем вещественных чисел называется вещественным векторным пространством.

Теорема. (Простейшие свойства векторных пространств.)

1. В векторном пространстве существует единственный нулевой вектор.

2. В векторном пространстве любой вектор имеет единственный противоположный ему.

3. или
.

4. .

Доказательство. 1) Единственность нулевого вектора доказывается также, как единственность единичной матриц и, вообще, как единственность нейтрального элемента любой внутренней бинарной алгебраической операции.

Пусть 0 – нулевой вектор векторного пространства V. Тогда . Пусть
– еще один нулевой вектор. Тогда . Возьмем в первом случае
, а во втором –
. Тогда
и
, откуда следует, что
, ч.т.д.

2а) Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.

Пусть
. Тогда, применяя аксиомы векторного пространства, получаем:

Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует

.

2б) Теперь докажем утверждение 4). Пусть
– произвольный вектор. Тогда

Отсюда сразу же следует, что вектор
является противоположным вектору х.

2в) Пусть теперь
. Тогда, применяя аксиомы векторного пространства,
и
получаем:

2г) Пусть
и допустим, что
. Так как
, где К – поле, то существует
. Умножим равенство
слева на
:
, откуда следует
или
или
.

Теорема доказана.

п.2. Примеры векторных пространств.

1) Множество числовых вещественных функций одной переменной, непрерывных на интервале (0; 1) относительно обычных операций сложения функций и умножения функции на число.

2) Множество многочленов от одной буквы с коэффициентами из поля K относительно сложения многочленов и умножения многочленов на скаляр.

3) Множество комплексных чисел относительно сложения комплексных чисел и умножения на действительное число.

4) Множество матриц одного и того же размера с элементами из поля К относительно сложения матриц и умножения матриц на скаляр.

Следующий пример является важным частным случаем примера 4.

5) Пусть - произвольное натуральное число. Обозначим через множество всех столбцов высоты n, т.е. множество матриц над полем K размера
.

Множество является векторным пространством над полем К и называется арифметическим векторным пространством столбцов высоты n над полем K.

В частности, если вместо произвольного поля К взять поле действительных чисел , то векторное пространство
называется вещественным арифметическим векторным пространством столбцов высоты n.

Аналогично, векторным пространством является и множество матриц над полем K размера
или, иначе, строк длины n. Оно обозначается также через и также называется арифметическим векторным пространством строк длины n над полем K.

п.3. Системы векторов векторного пространства.

Определение. Системой векторов векторного пространства называют любое конечное непустое множество векторов этого пространства.

Обозначение:
.

Определение. Выражение

, (1)

где - скаляры поля К, – векторы векторного пространства V, называется линейной комбинацией системы векторов
. Скаляры называются коэффициентами этой линейной комбинации.

Определение. Если все коэффициенты линейной комбинации (1) равны нулю, то такую линейную комбинацию называют тривиальной, в противном случае – нетривиальной.

Пример. Пусть
система из трех векторов векторного пространства V. Тогда

– тривиальная линейная комбинация данной системы векторов;

– нетривиальная линейная комбинация данной системы векторов, т.к. первый коэффициент этой комбинации
.

Определение. Если какой-либо вектор х векторного пространства V может быть представлен в виде:

то говорят, что вектор х линейно выражается через векторы системы
. В этом случае говорят также, что система
линейно представляет вектор х.

Замечание. В этом и предыдущем определении слово "линейно" часто пропускают и говорят, что система представляет вектор или вектор выражается через векторы системы и т.п.

Пример. Пусть
– система из двух столбцов арифметического вещественного векторного пространства столбцов высоты 2. Тогда столбец
линейно выражается через столбцы системы или данная система столбцов линейно представляет столбец х. Действительно,

п.4. Линейно зависимые и линейно независимые системы векторов векторного пространства.

Так как произведение нулевого скаляра на любой вектор есть нулевой вектор и сумма нулевых векторов равна нулевому вектору, то для любой системы векторов выполняется равенство

Отсюда следует, что нулевой вектор линейно выражается через векторы любой системы векторов или, говоря иначе, любая система векторов линейно представляет нулевой вектор.

Пример. Пусть
. В этом случае нулевой столбец можно линейно выразить через столбцы системы не одним способом:

или

Чтобы различать эти способы линейного представления нулевого вектора введем следующее определение.

Определение. Если выполняется равенство

и при этом все коэффициенты , то говорят, что система
представляет нулевой вектор тривиально. Если же в равенстве (3) хотя бы один из коэффициентов
не равен нулю, тогда говорят, что система векторов
представляет нулевой вектор нетривиально.

Из последнего примера мы видим, что существуют системы векторов, которые могут представлять нулевой вектор нетривиально. Из следующего примера мы увидим, что существуют системы векторов, которые не могут представлять нулевой вектор нетривиально.

Пример. Пусть
– система двух столбцов из векторного пространства . Рассмотрим равенство:

,

где
неизвестные пока коэффициенты. Используя правила умножения столбца на скаляр (число) и сложения столбцов, получаем равенство:

.

Из определения равенства матриц следует, что
и
.

Таким образом, данная система не может представлять нулевой столбец нетривиально.

Из приведенных примеров следует, что существует два вида систем векторов. Одни системы представляют нулевой вектор нетривиально, а другие нет. Отметим еще раз, что любая система векторов представляет нулевой вектор тривиально.

Определение. Система векторов векторного пространства, которая представляет нулевой вектор ТОЛЬКО тривиально называется линейно независимой.

Определение. Система векторов векторного пространства, которая может представить нулевой вектор нетривиально называется линейно зависимой.

Последнее определение можно дать в более развернутом виде.

Определение. Система векторов
векторного пространства V называется линейно зависимой, если найдется такой ненулевой набор скаляров поля K

Замечание. Любая система векторов
может представлять нулевой вектор тривиально:

Но этого недостаточно, чтобы выяснить линейно зависимая или же линейно независимая данная система векторов. Из определения следует, что линейно независимая система векторов не может представлять нулевой вектор нетривиально, а только тривиально. Поэтому для того, чтобы убедиться в линейной независимости данной системы векторов, нужно рассмотреть представление нуля произвольной линейной комбинацией этой системы векторов:

Если это равенство невозможно при условии, чтобы хотя бы один коэффициент этой линейной комбинации был ненулевой, тогда эта система является по определению линейно независимой.

Так в примерах предыдущего параграфа система столбцов
является линейно независимой, а система столбцов
является линейно зависимой.

Аналогично доказывается линейная независимость системы столбцов , , ... ,

из пространства , где К - произвольное поле, n – произвольное натуральное число.

Следующие теоремы дают несколько критериев линейной зависимости и соответственно линейной независимости систем векторов.

Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

Доказательство. Необходимость. Пусть система
линейно зависимая. Тогда, по определению, она представляет нулевой вектор нетривиально, т.е. существует нетривиальная линейная комбинация данной системы векторов равная нулевому вектору:

где хотя бы один из коэффициентов этой линейной комбинации не равен нулю. Пусть
,
.

Разделим обе части предыдущего равенства на этот ненулевой коэффициент (т.е. умножим на :

Обозначим:
, где .

т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.

Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:

Перенесем вектор в правую часть этого равенства:

Так как коэффициент при векторе равен
, то мы имеем нетривиальное представление нуля системой векторов
, что означает, что эта система векторов является линейно зависимой, ч.т.д.

Теорема доказана.

Следствие.

1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.

2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.

Доказательство.

1) Необходимость. Пусть система линейно независимая. Допустим противное и существует вектор системы линейно выражающийся через другие вектора этой системы. Тогда по теореме система является линейно зависимой и мы приходим к противоречию.

Достаточность. Пусть ни один из векторов системы не выражается через другие. Допустим противное. Пусть система линейно зависимая, но тогда из теоремы следует, что существует вектор системы линейно выражающийся через другие векторы этой системы и мы опять приходим к противоречию.

2а) Пусть система содержит нулевой вектор. Допустим для определенности, что вектор
:. Тогда очевидно равенство

т.е. один из векторов системы линейно выражается через другие вектора этой системы. Из теоремы следует, что такая система векторов является линейно зависимой, ч.т.д.

Заметим, что этот факт можно доказать непосредственно из определения линейно зависимой системы векторов.

Так как
, то следующее равенство очевидно

Это нетривиальное представление нулевого вектора, а значит система
является линейно зависимой.

2б) Пусть система имеет два равных вектора. Пусть для определенности
. Тогда очевидно равенство

Т.е. первый вектор линейно выражается через остальные векторы этой же системы. Из теоремы следует, что данная система линейно зависимая, ч.т.д.

Аналогично предыдущему это утверждение можно доказать и непосредственно определения линейно зависимой системы.

Действительно, так как
, то верно равенство

т.е. мы имеем нетривиальное представление нулевого вектора.

Следствие доказано.

Теорема (О линейной зависимости системы из одного вектора.

Система, состоящая из одного вектора является линейно зависимой тогда и только тогда, когда этот вектор нулевой.

Доказательство.

Необходимость. Пусть система
линейно зависимая, т.е. существует нетривиальное представление нулевого вектора

,

где
и
. Из простейших свойств векторного пространства следует, что тогда
.

Достаточность. Пусть система состоит из одного нулевого вектора
. Тогда эта система представляет нулевой вектор нетривиально

,

откуда следует линейная зависимость системы
.

Теорема доказана.

Следствие. Система, состоящая из одного вектора является линейно независимой тогда и только тогда, когда этот вектор ненулевой.

Доказательство оставляется читателю как упражнение.

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Определение 1

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Определение 2

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e (1) = (1 , 0 , . . . , 0) e (2) = (0 , 1 , . . . , 0) e (n) = (0 , 0 , . . . , 1)

Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e (1) , e (2) , . . . , e (n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e (1) , e (2) , . . . , e (n) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e (2) , e (1) , . . . , e (n) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e (2) , e (1) , . . . , e (n) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Определение 3

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Пример 1

Исходные данные: векторы

a = (3 , - 2 , 1) b = (2 , 1 , 2) c = (3 , - 1 , - 2)

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 - 2 1 - 1 1 2 - 2 A = 3 - 2 1 2 1 2 3 - 1 - 2 = 3 · 1 · (- 2) + (- 2) · 2 · 3 + 1 · 2 · (- 1) - 1 · 1 · 3 - (- 2) · 2 · (- 2) - 3 · 2 · (- 1) = = - 25 ≠ 0 ⇒ R a n k (A) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Пример 2

Исходные данные: векторы

a = (3 , - 2 , 1) b = (2 , 1 , 2) c = (3 , - 1 , - 2) d = (0 , 1 , 2)

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = (3 , - 2 , 1) , b = (2 , 1 , 2) , c = (3 , - 1 , - 2) является базисом.

Ответ: указанная система векторов не является базисом.

Пример 3

Исходные данные: векторы

a = (1 , 2 , 3 , 3) b = (2 , 5 , 6 , 8) c = (1 , 3 , 2 , 4) d = (2 , 5 , 4 , 7)

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7 ~ 1 2 3 3 0 1 0 2 0 1 - 1 1 0 1 - 2 1 ~ ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 - 2 - 1 ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 0 1 ⇒ ⇒ R a n k (A) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Пример 4

Исходные данные: векторы

a (1) = (1 , 2 , - 1 , - 2) a (2) = (0 , 2 , 1 , - 3) a (3) = (1 , 0 , 0 , 5)

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e (1) , e (2) , . . . , e (n) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Определение 4

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Доказательство 1

Докажем эту теорему:

зададим базис n -мерного векторного пространства - e (1) , e (2) , . . . , e (n) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e:

x = x 1 · e (1) + x 2 · e (2) + . . . + x n · e (n) , где x 1 , x 2 , . . . , x n - некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

x = x ~ 1 e (1) + x 2 ~ e (2) + . . . + x ~ n e (n) , где x ~ 1 , x ~ 2 , . . . , x ~ n - некие числа.

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e (1) + x 2 · e (2) + . . . + x n · e (n) . Получим:

0 = (x ~ 1 - x 1) · e (1) + (x ~ 2 - x 2) · e (2) + . . . (x ~ n - x n) · e (2)

Система базисных векторов e (1) , e (2) , . . . , e (n) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты (x ~ 1 - x 1) , (x ~ 2 - x 2) , . . . , (x ~ n - x n) будут равны нулю. Из чего справедливым будет: x 1 = x ~ 1 , x 2 = x ~ 2 , . . . , x n = x ~ n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e (1) , e (2) , . . . , e (n) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = (x 1 , x 2 , . . . , x n) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

а также задан вектор x = (x 1 , x 2 , . . . , x n) .

Векторы e 1 (1) , e 2 (2) , . . . , e n (n) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 (1) , e 2 (2) , . . . , e n (n) , обозначаемые как x ~ 1 , x ~ 2 , . . . , x ~ n .

Вектор x → будет представлен следующим образом:

x = x ~ 1 · e (1) + x ~ 2 · e (2) + . . . + x ~ n · e (n)

Запишем это выражение в координатной форме:

(x 1 , x 2 , . . . , x n) = x ~ 1 · (e (1) 1 , e (1) 2 , . . . , e (1) n) + x ~ 2 · (e (2) 1 , e (2) 2 , . . . , e (2) n) + . . . + + x ~ n · (e (n) 1 , e (n) 2 , . . . , e (n) n) = = (x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + . . . + x ~ n e 1 (n) , x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + + . . . + x ~ n e 2 (n) , . . . , x ~ 1 e n (1) + x ~ 2 e n (2) + . . . + x ~ n e n (n))

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x ~ 1 , x ~ 2 , . . . , x ~ n:

x 1 = x ~ 1 e 1 1 + x ~ 2 e 1 2 + . . . + x ~ n e 1 n x 2 = x ~ 1 e 2 1 + x ~ 2 e 2 2 + . . . + x ~ n e 2 n ⋮ x n = x ~ 1 e n 1 + x ~ 2 e n 2 + . . . + x ~ n e n n

Матрица этой системы будет иметь следующий вид:

e 1 (1) e 1 (2) ⋯ e 1 (n) e 2 (1) e 2 (2) ⋯ e 2 (n) ⋮ ⋮ ⋮ ⋮ e n (1) e n (2) ⋯ e n (n)

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 (1) , e 2 (2) , . . . , e n (n) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x ~ 1 , x ~ 2 , . . . , x ~ n вектора x → в базисе e 1 (1) , e 2 (2) , . . . , e n (n) .

Применим рассмотренную теорию на конкретном примере.

Пример 6

Исходные данные: в базисе трехмерного пространства заданы векторы

e (1) = (1 , - 1 , 1) e (2) = (3 , 2 , - 5) e (3) = (2 , 1 , - 3) x = (6 , 2 , - 7)

Необходимо подтвердить факт, что система векторов e (1) , e (2) , e (3) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e (1) , e (2) , e (3) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e (1) , e (2) , e (3) .

Используем метод Гаусса:

A = 1 - 1 1 3 2 - 5 2 1 - 3 ~ 1 - 1 1 0 5 - 8 0 3 - 5 ~ 1 - 1 1 0 5 - 8 0 0 - 1 5

R a n k (A) = 3 . Таким образом, система векторов e (1) , e (2) , e (3) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x ~ 1 , x ~ 2 , x ~ 3 . Связь этих координат определяется уравнением:

x 1 = x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + x ~ 3 e 1 (3) x 2 = x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + x ~ 3 e 2 (3) x 3 = x ~ 1 e 3 (1) + x ~ 2 e 3 (2) + x ~ 3 e 3 (3)

Применим значения согласно условиям задачи:

x ~ 1 + 3 x ~ 2 + 2 x ~ 3 = 6 - x ~ 1 + 2 x ~ 2 + x ~ 3 = 2 x ~ 1 - 5 x ~ 2 - 3 x 3 = - 7

Решим систему уравнений методом Крамера:

∆ = 1 3 2 - 1 2 1 1 - 5 - 3 = - 1 ∆ x ~ 1 = 6 3 2 2 2 1 - 7 - 5 - 3 = - 1 , x ~ 1 = ∆ x ~ 1 ∆ = - 1 - 1 = 1 ∆ x ~ 2 = 1 6 2 - 1 2 1 1 - 7 - 3 = - 1 , x ~ 2 = ∆ x ~ 2 ∆ = - 1 - 1 = 1 ∆ x ~ 3 = 1 3 6 - 1 2 2 1 - 5 - 7 = - 1 , x ~ 3 = ∆ x ~ 3 ∆ = - 1 - 1 = 1

Так, вектор x → в базисе e (1) , e (2) , e (3) имеет координаты x ~ 1 = 1 , x ~ 2 = 1 , x ~ 3 = 1 .

Ответ: x = (1 , 1 , 1)

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c (1) = (c 1 (1) , c 2 (1) , . . . , c n (1)) c (2) = (c 1 (2) , c 2 (2) , . . . , c n (2)) ⋮ c (n) = (c 1 (n) , e 2 (n) , . . . , c n (n))

e (1) = (e 1 (1) , e 2 (1) , . . . , e n (1)) e (2) = (e 1 (2) , e 2 (2) , . . . , e n (2)) ⋮ e (n) = (e 1 (n) , e 2 (n) , . . . , e n (n))

Указанные системы являются также базисами заданного пространства.

Пусть c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1) - координаты вектора c (1) в базисе e (1) , e (2) , . . . , e (3) , тогда связь координат будет задаваться системой линейных уравнений:

с 1 (1) = c ~ 1 (1) e 1 (1) + c ~ 2 (1) e 1 (2) + . . . + c ~ n (1) e 1 (n) с 2 (1) = c ~ 1 (1) e 2 (1) + c ~ 2 (1) e 2 (2) + . . . + c ~ n (1) e 2 (n) ⋮ с n (1) = c ~ 1 (1) e n (1) + c ~ 2 (1) e n (2) + . . . + c ~ n (1) e n (n)

В виде матрицы систему можно отобразить так:

(c 1 (1) , c 2 (1) , . . . , c n (1)) = (c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1)) · e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

Сделаем по аналогии такую же запись для вектора c (2) :

(c 1 (2) , c 2 (2) , . . . , c n (2)) = (c ~ 1 (2) , c ~ 2 (2) , . . . , c ~ n (2)) · e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

(c 1 (n) , c 2 (n) , . . . , c n (n)) = (c ~ 1 (n) , c ~ 2 (n) , . . . , c ~ n (n)) · e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

Матричные равенства объединим в одно выражение:

c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n) = c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) · e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n)

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e (1) , e (2) , . . . , e (3) через базис c (1) , c (2) , . . . , c (n) :

e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n) = e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) · c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n)

Дадим следующие определения:

Определение 5

Матрица c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) является матрицей перехода от базиса e (1) , e (2) , . . . , e (3)

к базису c (1) , c (2) , . . . , c (n) .

Определение 6

Матрица e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) является матрицей перехода от базиса c (1) , c (2) , . . . , c (n)

к базису e (1) , e (2) , . . . , e (3) .

Из этих равенств очевидно, что

c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) · e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) · c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1

т.е. матрицы перехода взаимообратны.

Рассмотрим теорию на конкретном примере.

Пример 7

Исходные данные: необходимо найти матрицу перехода от базиса

c (1) = (1 , 2 , 1) c (2) = (2 , 3 , 3) c (3) = (3 , 7 , 1)

e (1) = (3 , 1 , 4) e (2) = (5 , 2 , 1) e (3) = (1 , 1 , - 6)

Также нужно указать связь координат произвольного вектора x → в заданных базисах.

Решение

1. Пусть T – матрица перехода, тогда верным будет равенство:

3 1 4 5 2 1 1 1 1 = T · 1 2 1 2 3 3 3 7 1

Умножим обе части равенства на

1 2 1 2 3 3 3 7 1 - 1

и получим:

T = 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1

2. Определим матрицу перехода:

T = 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 = = 3 1 4 5 2 1 1 1 - 6 · - 18 5 3 7 - 2 - 1 5 - 1 - 1 = - 27 9 4 - 71 20 12 - 41 9 8

3. Определим связь координат вектора x → :

допустим, что в базисе c (1) , c (2) , . . . , c (n) вектор x → имеет координаты x 1 , x 2 , x 3 , тогда:

x = (x 1 , x 2 , x 3) · 1 2 1 2 3 3 3 7 1 ,

а в базисе e (1) , e (2) , . . . , e (3) имеет координаты x ~ 1 , x ~ 2 , x ~ 3 , тогда:

x = (x ~ 1 , x ~ 2 , x ~ 3) · 3 1 4 5 2 1 1 1 - 6

Т.к. равны левые части этих равенств, мы можем приравнять и правые:

(x 1 , x 2 , x 3) · 1 2 1 2 3 3 3 7 1 = (x ~ 1 , x ~ 2 , x ~ 3) · 3 1 4 5 2 1 1 1 - 6

Умножим обе части справа на

1 2 1 2 3 3 3 7 1 - 1

и получим:

(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 ⇔ ⇔ (x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · T ⇔ ⇔ (x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · - 27 9 4 - 71 20 12 - 41 9 8

С другой стороны

(x ~ 1 , x ~ 2 , x ~ 3) = (x 1 , x 2 , x 3) · - 27 9 4 - 71 20 12 - 41 9 8

Последние равенства показывают связь координат вектора x → в обоих базисах.

Ответ: матрица перехода

27 9 4 - 71 20 12 - 41 9 8

Координаты вектора x → в заданных базисах связаны соотношением:

(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · - 27 9 4 - 71 20 12 - 41 9 8

(x ~ 1 , x ~ 2 , x ~ 3) = (x 1 , x 2 , x 3) · - 27 9 4 - 71 20 12 - 41 9 8 - 1

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

ВЕКТОРНОЕ ПРОСТРАНСТВО (линейное пространство), одно из фундаментальных понятий алгебры, обобщающее понятие совокупности (свободных) векторов. В векторном пространстве вместо векторов рассматриваются любые объекты, которые можно складывать и умножать на числа; при этом требуется, чтобы основные алгебраические свойства этих операций были такими же, как и для векторов в элементарной геометрии. В точном определении числа заменяются элементами любого поля К. Векторным пространством над полем К называется множество V с операцией сложения элементов из V и операцией умножения элементов из V на элементы из поля К, которые обладают следующими свойствами:

х + у = у + х для любых х, у из V, т. е. относительно сложения V является абелевой группой;

λ(х + у) = λ χ + λу для любых λ из К и х, у из V;

(λ + μ)х = λх + μх для любых λ, μ из К и х из V;

(λ μ)х = λ(μх) для любых λ, μ из К и х из V;

1х = х для любого х из V, здесь 1 означает единицу поля К.

Примерами векторного пространства являются: множества L 1 , L 2 и L 3 всех векторов из элементарной геометрии, соответственно на прямой, плоскости и в пространстве с обычными операциями сложения векторов и умножения на число; координатное векторному пространству K n , элементами которого являются всевозможные строки (векторы) длины n с элементами из поля К, а операции заданы формулами

множество F(M, К) всех функций, оп-ределённых на фиксированном множе-стве М и принимающих значения в поле К, с обычными операциями над функ-циями:

Элементы векторного пространства е 1 ..., е n называются линейно независимыми, если из равенства λ 1 e 1 + ... +λ n е n = 0 Є V следует, что все λ 1 , λ 2 ,..., λ n = 0 Є К. В противном слу-чае элементы е 1 , е 2 , ···> е n называются линейно зависимыми. Если в векторном пространстве V любые n + 1 элементов e 1 ,..., е n+1 ли-нейно зависимы и существует n линей-но независимых элементов, то V назы-вается n-мерным векторным пространством, а n - размерно-стью векторного пространства V. Если в векторном пространстве V для любого натурального n существует n линейно независимых векторов, то V называется бесконечномерным векторным пространством. Например, векторное пространство L 1 , L 2 , L 3 и К n соответственно 1-, 2-, 3- и n-мерны; если М - бесконечное множество, то векторное пространство F(М, К) бесконечномерно.

Векторное пространство V и U над полем К называются изоморфными, если существует взаимно однозначное отображение φ : V -> U такое, что φ(х+у) = φ(х) + φ(у) для любых х, у из V и φ(λх) = λ φ(х) для любых λ из К и х из V. Изоморфные векторные пространства являются алгебраически неразличимыми. Классификация конечномерных векторных пространств с точностью до изоморфности даётся их размерностью: любое n-мерное векторное пространство над полем К изоморфно координатному векторному пространству К n . Смотри также Гильбертово пространство, Линейная алгебра.